根据地形的点云抽稀算法的 Python 实现

背景

什么是点云

点云是空间中一系列的点，每个点有空间中的 X、Y、Z 坐标。通过一系列的点构成的点云，描绘出地形的一种数据。在使用无人机做地形测量中，由无人机拍摄的照片经过摄影测量计算，最终输出的一种典型格式就是点云格式。

为什么要根据地形抽稀

在通过摄影测量输出的点云中，数量级是通常的地形处理软件（如 CAD）无法处理的，以国内用的比较多的 CASS 为例，处理由几万点组成的地形数据，已经达到极限。因为之前这些软件适配的都是通过人工在地形上进行采集数据点，人工一般间隔 3-5 米采集一个点。而无人机输出的点云间隔可以在 5cm 甚至更低。
在常规的处理流程中，一般先将无人机输出的点云，经过专业软件识别地形与非地形（剔除建筑，车辆，植被点云），保留地形点，再将地形点按距离平均抽稀成 0.5 米一个点左右。而此时点数可能依然在几十万级别。接下去的抽稀就要考虑地形因素，一般来说需要保证 3-5 米一个点。同时，在地形平缓的部分，可以适当稀疏，在地形起伏部分，需要适当加密。以保证在足够少的点数下，同样可以描绘出地形。确保后续处理算量的准确度。

核心思想

• 读取点云
• alphashape 算法，取范围点
• 创建三角网
• 去除三角网中内角有大于 120 度的三角形
• 将整幅图划分 3*3 米网格(用于确保每个网格中都存在点，防止在平整地区全部判断为非关键点，被去除)
• 遍历每个点
• 如果点判断为范围点，直接保留，对该点所处的网格标记，继续遍历
• 如果点判断为非范围点，找到以该点为顶点的所有三角形
• 计算空间三角形的面的法向量
• 判断每个空间三角形所在的面的法向量夹角
• 如果存在某个法向量夹角大于一个阈值，即判定该点为关键点，保留，对该点所处的网格标记，继续遍历
• 判断即非范围点，也非关键点，则去除
• 检查是否每个网格都有至少一个点，如没有，找点放入

代码实现

读取点云

这边读取的是 dat 格式的点云文件

def readDAT(path):
    point_list = []
    with open(path) as f:
        line = f.readline()
        while line:
            str_list = line.rstrip().split(',')
            point = [float(str_list[2]), float(str_list[3]), float(str_list[4])]
            point_list.append(point)
            line = f.readline()
    return point_list

alphashape 算法，取范围点

具体可参考 https://github.com/bellockk/alphashape ，这里只做了调用
PS：其实在这个抽稀算法中，alphashape 不重要，因为后续每 3*3m 网格会包含一个点，是否取到点的范围线问题不大

def find_shape(self, alpha=0.15):
    points_2d = [(self.points[i][0], self.points[i][1]) for i in range(len(self.points))]
    # alpha_shape = alphashape.alphashape(points)
    alpha_shape = alphashape.alphashape(points_2d, alpha=alpha)

    if type(alpha_shape) == Polygon:
        x, y = alpha_shape.exterior.coords.xy
        self.shape_points = [[x[i], y[i]] for i in range(len(x))]
        return True, '查找范围成功'
    else:
        print('查找范围失败，减小 alpha 值')
        return False, '查找范围失败，减小 alpha 值'

创建三角网

参考：https://github.com/HakanSeven12/Delaunator-Python， 这里只做调用

def create_coordinates(self):
    triangles = Delaunator(self.points).triangles
    # halfedges = Delaunator(self.points).halfedges
    # hull = Delaunator(self.points).hull
    # coords = Delaunator(self.points).coords
    coordinates = []
    for i in range(0, len(triangles), 3):
        coordinates.append([
            self.points[triangles[i]],
            self.points[triangles[i + 1]],
            self.points[triangles[i + 2]]])
    self.coordinates = coordinates

去除三角网中内角有大于 120 度的三角形

遍历三角形，根据每个三角形的平面坐标计算三个内角

def clean_above_120_coordinate(self):
    new_coordinates = []
    for coordinate in self.coordinates:
        a = math.sqrt((coordinate[0][0] - coordinate[1][0]) * (coordinate[0][0] - coordinate[1][0]) +
                      (coordinate[0][1] - coordinate[1][1]) * (coordinate[0][1] - coordinate[1][1]))
        b = math.sqrt((coordinate[1][0] - coordinate[2][0]) * (coordinate[1][0] - coordinate[2][0]) +
                      (coordinate[1][1] - coordinate[2][1]) * (coordinate[1][1] - coordinate[2][1]))
        c = math.sqrt((coordinate[2][0] - coordinate[0][0]) * (coordinate[2][0] - coordinate[0][0]) +
                      (coordinate[2][1] - coordinate[0][1]) * (coordinate[2][1] - coordinate[0][1]))
        A = math.degrees(math.acos(clamp((a * a - b * b - c * c) / (-2 * b * c), -1, 1)))  # 夹角1
        B = math.degrees(math.acos(clamp((b * b - a * a - c * c) / (-2 * a * c), -1, 1)))  # 夹角2
        C = math.degrees(math.acos(clamp((c * c - a * a - b * b) / (-2 * a * b), -1, 1)))  # 夹角3

        # print(A, B, C)
        if A >= 120 or B >= 120 or C >= 120:
            continue
        new_coordinates.append(coordinate)
    self.coordinates_without120 = new_coordinates

去除 120 度三角网后的地形三角网，黑线为 AlphaShape 取出的范围

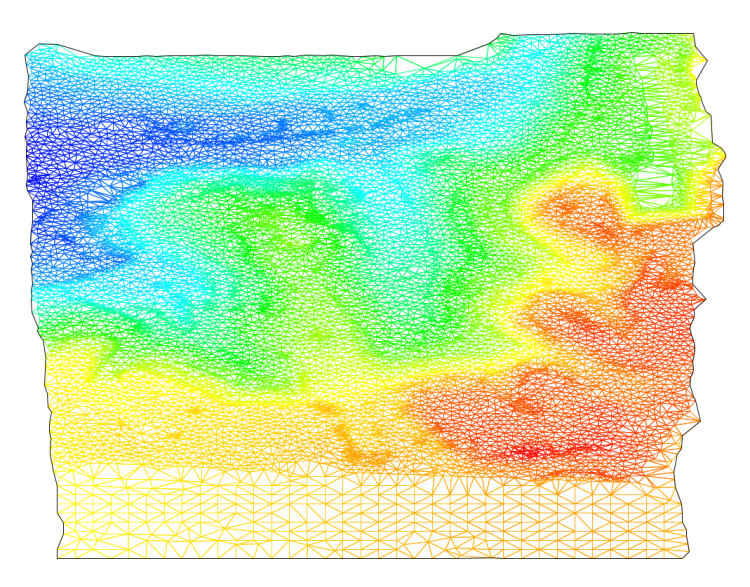
将整幅图划分 3*3 米网格

(用于确保每个网格中都存在点，防止在平整地区全部判断为非关键点，被去除)

def init_grid(self, distance=3.5):
    # self.x_y_min_max 是平面上最上下左右的范围
    distance_x = self.x_y_min_max[1] - self.x_y_min_max[0]
    distance_y = self.x_y_min_max[3] - self.x_y_min_max[2]
    num_x = distance_x // distance
    num_y = distance_y // distance
    num_x += 1
    num_y += 1
    grid = [[False for i in range(int(num_x))] for j in range(int(num_y))]
    return grid

核心流程（遍历、判断、抽稀）

def thinning_task(self, limit_angle, limit_distance, points):
    self.grid = self.init_grid(distance=limit_distance)
    new_points = []
    for point in points:
        # 判断是否为边界点
        if is_point_in_shape(point, self.shape_points):
            new_points.append(point)
            self.set_grid(point, limit_distance)
            continue
        # 找到以该点为顶点的三角形
        coordinates_with_point = search_coordinates_with_point(self.coordinates_without120, point)
        if len(coordinates_with_point) == 0:
            continue
        # 判断是否为特征点
        if is_characteristic_point(coordinates_with_point, limit_angle):
            new_points.append(point)
            self.set_grid(point, limit_distance)
    # 补齐网格点
    for point in points:
        # 判断这个点所处的格子里是否有点了
        if self.is_grid_false(point, limit_distance) is False:
            new_points.append(point)
            self.set_grid(point, limit_distance)
    return new_points

• 如果点判断为范围点，直接保留，对该点所处的网格标记，继续遍历

def is_point_in_shape(point, shape_points):
    if shape_points is None:
        return False
    for shape_point in shape_points:
        if point[0] == shape_point[0] and point[1] == shape_point[1]:
            return True
    return False

• 如果点判断为非范围点，找到以该点为顶点的所有三角形

原来的代码

def search_coordinates_with_point(coordinates, point):
    # 找到以该点为顶点的三角形
    coordinates_with_point = []
    for coordinate in coordinates:
        for coordinate_point in coordinate:
            if coordinate_point[0] == point[0] and coordinate_point[1] == point[1]:
                coordinates_with_point.append(coordinate)
    return coordinates_with_point

因为效率低下，后来使用 Python 内置数据库 SQLite 用于存点和找点，速度大幅提升

def search_coordinates_with_point(self, point):
    # 找到以该点为顶点的三角形
    coordinates_with_point = []
    cur = self.con.cursor()
    for i in range(1, 4):
        cur.execute('select * from test where x%s=? and y%s=?' % (i, i), (point[0], point[1]))
        results = cur.fetchall()
        for r in results:
            # print(r)
            coordinate = [[r[0], r[1], r[2]], [r[3], r[4], r[5]], [r[6], r[7], r[8]]]
            coordinates_with_point.append(coordinate)
    return coordinates_with_point

• 判断是否为特征点

（计算该点为顶点的三角形的面的法向量，判断法向量之间的夹角）

def is_characteristic_point(coordinates_with_point, limit_angle):
    range_angle1 = limit_angle
    range_angle2 = 180 - limit_angle
    vectors = []
    for coordinate in coordinates_with_point:
        # 计算每个三角形的空间法向量
        flag, dx, dy, dz = nv.CalNormalVector(coordinate[0][0], coordinate[0][1], coordinate[0][2],
                                              coordinate[1][0], coordinate[1][1], coordinate[1][2],
                                              coordinate[2][0], coordinate[2][1], coordinate[2][2])
        if flag:
            vectors.append((dx, dy, dz))
    for i in range(len(vectors)):
        # 只要有一个任意两个空间法向量直接的夹角大于 limit_angle，即判断这个点为特征点，保留
        # break_flag = False
        for j in range(len(vectors)):
            if i == j:
                continue
            angle = nv.CalAngle(vectors[i], vectors[j])
            # print(angle)
            if range_angle1 < angle < range_angle2:
                return True
    return False

• 检查是否每个网格都有至少一个点，如没有，找点放入

def set_grid(self, point, distance):
    index_x = int((point[0] - self.x_y_min_max[0]) // distance)
    index_y = int((point[1] - self.x_y_min_max[2]) // distance)
    self.grid[index_y][index_x] = True
    pass

def is_grid_false(self, point, distance):
    index_x = int((point[0] - self.x_y_min_max[0]) // distance)
    index_y = int((point[1] - self.x_y_min_max[2]) // distance)
    return self.grid[index_y][index_x]

数据验证

8wpoint.dat (limit_angle=8, limit_distance=3) 测试数据
抽稀前

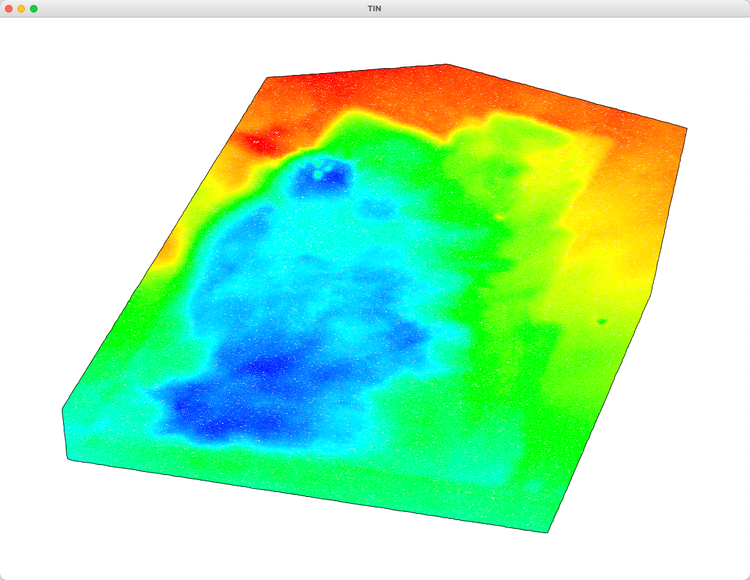
抽稀后

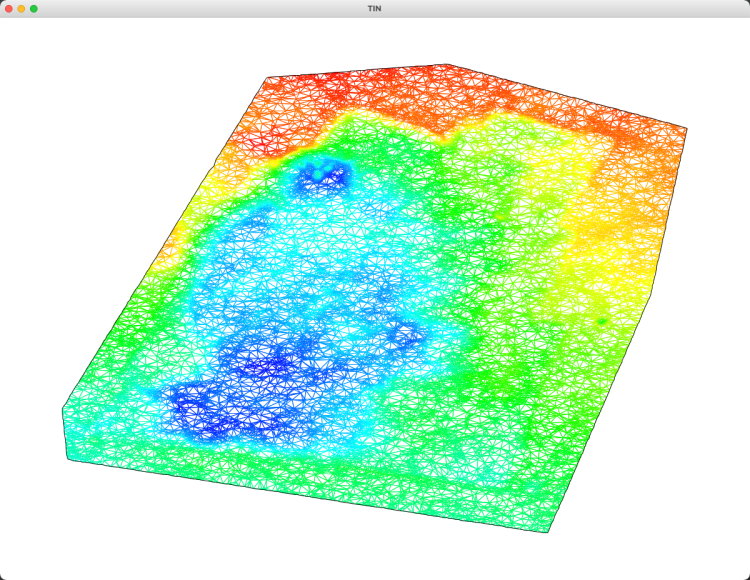
test.dat (limit_angle=10, limit_distance=5) 测试数据
抽稀前

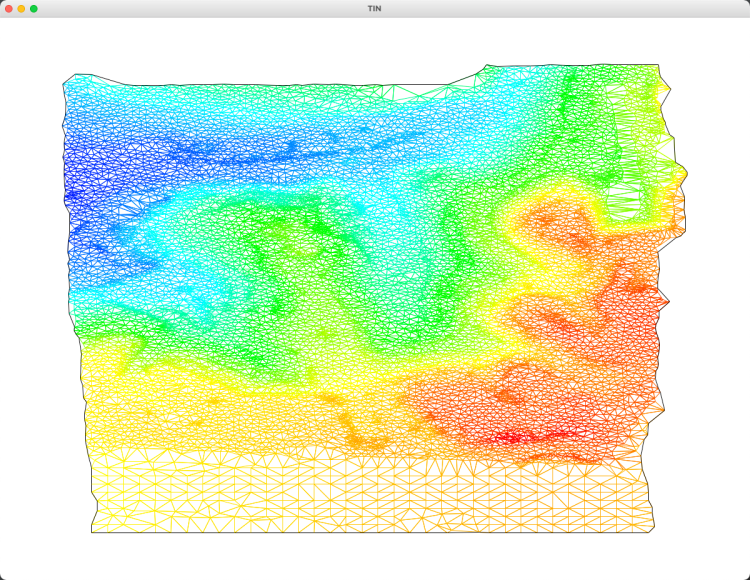
抽稀后

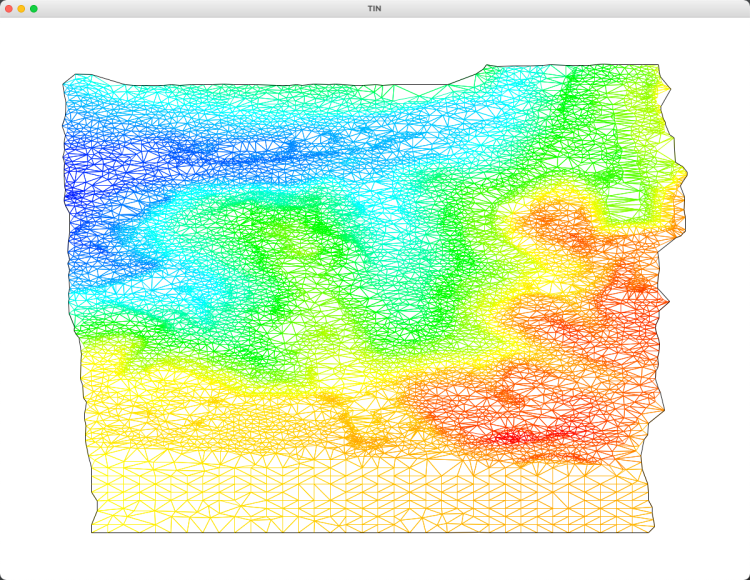
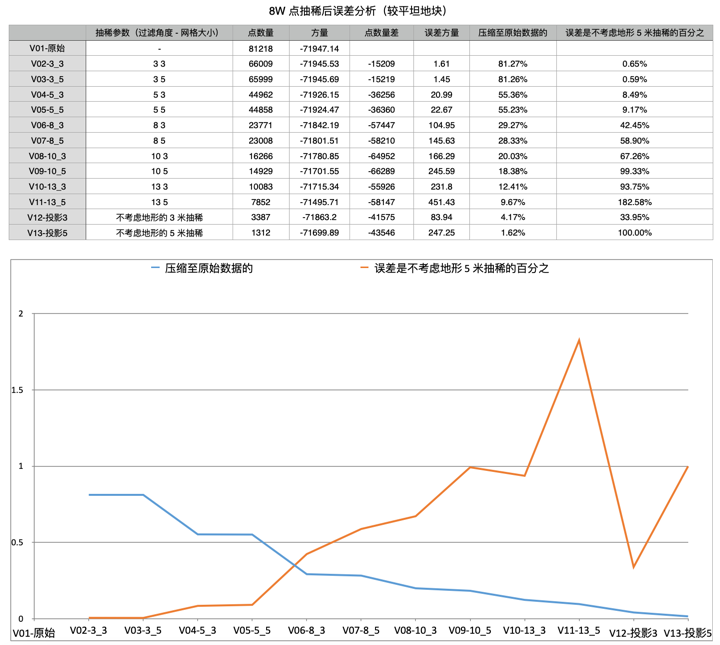
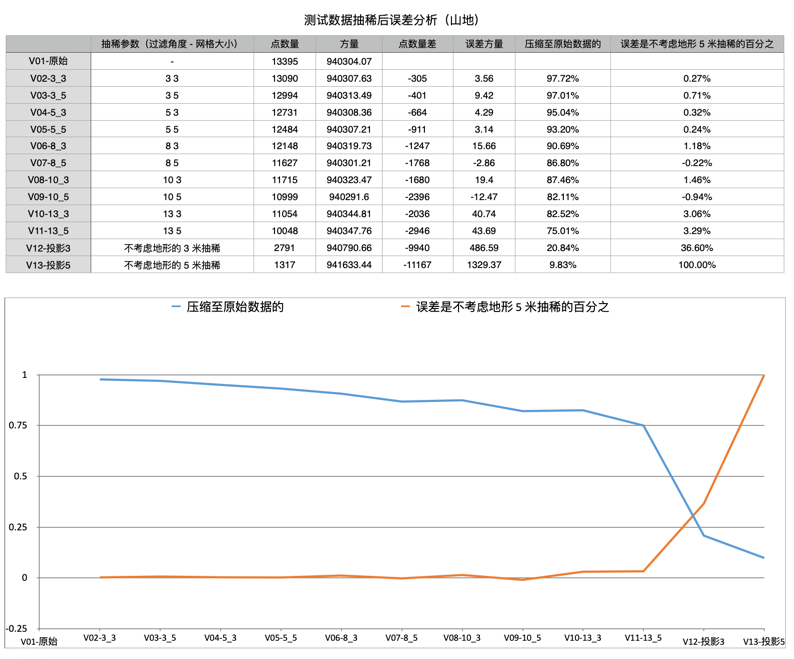
误差分析